태그

[Algorithm] 알고리즘과 자료구조

​
STUDY NOTE
개발을 하며 배우고 익힌 기술 / 개념을 남겨놓는 공간입니다.
잘못되거나 더 나은 지식이나, 코드에 대한 피드백은 언제나 환영입니다.
​
알고리즘?
어떠한 문제를 해결하기 위해 일련의 절차를 공식화한 형태로 표현한 것이며,
프로그래밍 알고리즘으로 해석한다면 input 값을 통해 output 값을 얻기 위한 계산 과정을 말한다.
​
​
​
* 좋은 알고리즘의 특징
정지 문제의 결과로 알고리즘이 정지하는데 걸리는 시간을 일반적으로 측정할 수는 없다.
그러므로 알고리즘에 대한 단순한 직관을 만족하는 형식적인 정의는 불가능하다.
따라서 알고리즘의 공식적인 정의는 없다.
​
대부분의 알고리즘은 유한한 수의 규칙에 따라 구별 가능한 기호들을 조작하여 input에서 output 을 생성하기 위한 일반화된 작업을 정의한다.
​
· 입력 : 외부에서 제공되는 0개 이상의 자료가 존재하며, 정의된 입력을 받아들일 수 있어야 한다.
· 출력 : 적어도 2개 이상의 서로 다른 결과를 내어야 한다. 즉, 모든 입력에 하나의 출력이 나오면 안 된다.
· 명확성 : 수행 과정은 명확하고 모호하지 않은 명령어로 구성되어야 한다.
- 정밀성 : 변하지 않는 명확한 작업 단계를 가져야 한다.
- 유일성 : 각 단계마다 명확한 다음 단계를 가져야 한다.
· 유한성 : 특정 수의 작업 이후 유한 시간 내에 종료한다.
· 효율성 : 모든 과정은 명백하게 실행 가능 (검증 가능) 한 것이어야 한다.
· 일반성 : 정의된 입력들에 일반적으로 적용할 수 있어야 한다.
​
​
* 알고리즘 개발의 정형적인 단계
문제 정의 → 모델 고안 → 명세 작성 → 설계 → 검증 → 분석(복잡도 등) → 구현 → 테스트 → 문서화
​
​
* 알고리즘에 필요한 기본 개념
1) 시간 복잡도
2) 자료의 구조
3) 정렬
​
​
시간 복잡도?
문제를 해결하는 데 걸리는 시간과 입력의 함수 관계
​
시간 복잡도 : 얼마나 빠른가?
공간 복잡도 : 얼마나 메모리를 적게 쓰는가?
=> 시간 복잡도를 더 중요시한다.
​
시간 복잡도를 나타낼 때는 Big O라는 표기법을 이용한다. 예를 들어서, 1부터 N까지의 합을 구한다고 할 때, 다음과 같은 두 가지 방법이 있다.​
// 방법 1 #include <cstudio> int main(void){ int N,res = 0; scanf("%d%, &N); for (int i=1; i<=N; i++){ res += i; } printf("%f\n, res); return 0; }
// 방법 2 #include <cstudio> int main(void){ int N,res; scanf("%d%, &N); res = N * (N+1) / 2; printf("%f\n, res); return 0; }
소스 1에서는 for 문을 활용하여 직접 res에 1에서 N까지 더해서 합을 합산했다. 그렇다면 N이 100이면 덧셈이 100번 일어나고, N이 10,000이면 덧셈이 10,000번 일어나게 된다. 즉, 계산 횟수가 N에 비례하게 된다.
반면에 소스 2에서는 수학공식을 사용하여 N이 100이여도 곱셈 한번, 덧셈 한번, 나눗셈 한 번을 사용하고, N이 10,000이여도 곱셈, 덧셈, 나눗셈을 각 한 번씩만 사용하면 계산을 할 수 있다.
​
따라서 소스 1은 Big O 표기법에 의해 O(n)의 시간 복잡도를 소스 2는 O(1)의 시간 복잡도가 사용된다.
시간 복잡도
설명
O(1)
상수 형태. n의 값에 상관없이 일정한 양의 계산만 한다.
O(log n)
로그 형태
O(n)
선형
O(nlogn)
선형 로그 형태
O(n^2),O(n^3),...
다 차 형태
O(2^n)
지수 형태
O(n!)
팩토리얼 형태
​
​
​
​
자료 구조?
데이터 사이의 관계를 반영한 저장 구조 및 그 조작 방법을 뜻한다.
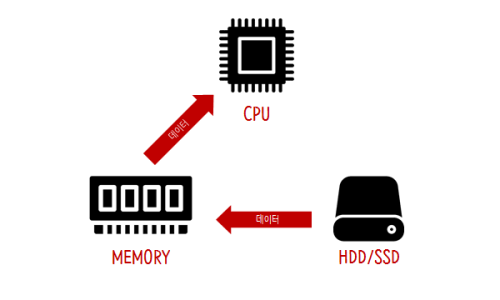
컴퓨터의 프로그램을 실행하면 CPU에서 메모리로 데이터를 이동해서 처리하는데, 이때 메모리를 효율적으로 사용하기 위해서는 데이터에 맞는 특성의 자료구조를 사용하는 것이 중요하다.
​
​
알고리즘
"프로그램이란 데이터를 표현하고, 그렇게 표현된 데이터를 처리하는 것이다."
자료구조
int main(void){ // 배열의 선언 = 자료구조 int arr[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; // 배열에 저장된 값의 합 = 알고리즘 for(idx=0; idx<10; idx++){ sum += arr[idx]; } }
※알고리즘은 자료구조에 의존적이다!
​
​
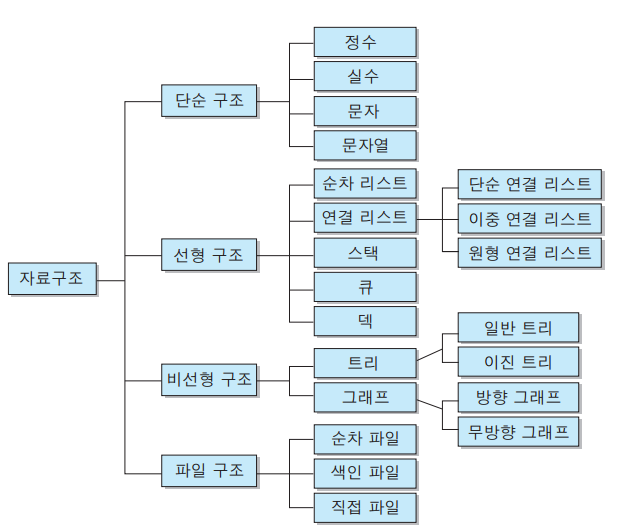
자료구조를 모두 나열하여 분류한다면 아래 표와 같이 볼 수 있다.
​
​
​
- 선형 구조 : 한 종류의 데이터가 선처럼 길게 나열된 자료구조
- 배열 : 가장 쉬운 자료구조이자 언어에 따라 활용법이 가장 크게 달라지는 자료구조
- 해시 : 해시는 해시 함수로 구현한다. 마치 배열처럼, 어떤 자료를 찾을 때 O(1)의 시간만을 소요하며, 해시 함수에 키값을 넣어 주솟값을 얻고
그 주소에 위치한 버킷에 저장된 데이터를 가져오는 방식을 사용한다. 하지만, 언제나 O(1)이 보장되는 것은 아니다.
- 스택 : 먼저 들어간 자료가 나중에 나오는 자료구조
- 큐 : 먼저 들어간 자료가 먼저 나오는 자료구조
- 덱 : 간단하게 말하자면 스택과 큐의 융합형태. 양쪽 끝에서 삽입과 삭제 모두가 가능하다.
​
- 비선형 구조 : 선형 자료구조가 아닌 모든 자료구조(i 번째 값을 탐색한 뒤의 i+1의 값이 정해지지 않은 구조)
- 그래프 : 함수의 그래프와는 전혀 다르다. 점들, 그리고 점들을 연결하는 선들 만으로 이루어진 지도를 연상하면 편하다.
이때의 점을 정점, 선을 간선이라고 부른다.
- 트리 : 그래프의 일종으로 트리에서 정점을 특별히 노드라고 하고, 간선을 가지라고 한다.
​
​
​
​
정렬?
크기순, 사전순과 같이 정렬하는 알고리즘을 말한다. 효율적인 알고리즘들 중 대부분은 데이터가 사전에 정렬되어 있을 것을 요구하는 것이 많다. 또한, 정렬 알고리즘은 알고리즘의 기초 중의 기초이면서도 널리 쓰이는 알고리즘이다.
​
1. 버블 정렬(Bubble sort)
가장 쉽지만, 시간 복잡도가 높아 효율적이지 않다.
시간 복잡도는 O(n^2)이며 공간 복잡도는 하나의 배열만 사용하여 정렬을 진행하기 때문에 O(n)이다.
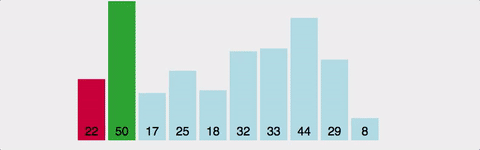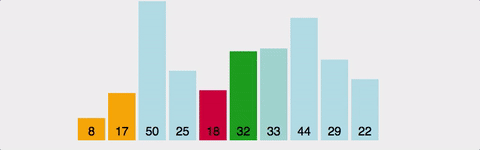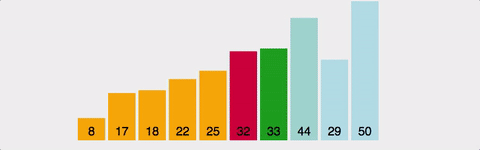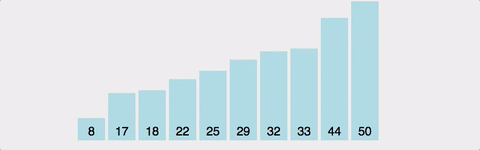
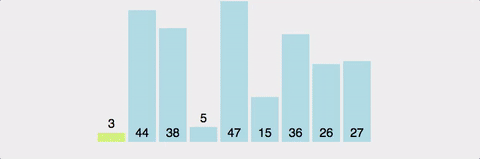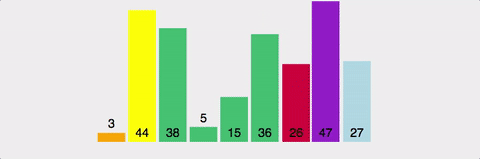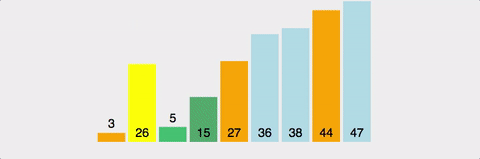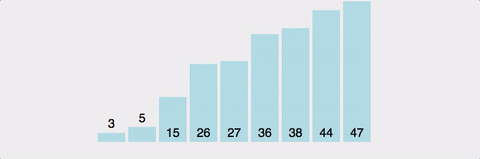
def bubbleSort(alist) : for loop_count in range(len(alist)-1,0,-1) : for idx in range(loop_count) : if alist[idx] > alist[idx+1] : tmp = alist[idx] alist[idx] = alist[idx+1] alist[idx+1] = tmp return alist
​
2. 선택 정렬(Selection sort)
선택 정렬은 시간 복잡도가 O(n^2)으로 버블 정렬과
알고리즘이 유사하다. 가장 큰 수를 찾아 배열의 마지막 위치와 교환한다.
def selectionSort(alist): for offset in range(0,len(alist)-1): offset_minValue = offset for num in range(offset+1, len(alist)): if alist[num] < alist[offset_minValue]: offset_minValue = num tmp = alist[offset_minValue] alist[offset_minValue] = alist[offset] alist[offset] = tmp return alist
​
3. 삽입 정렬(Insertion sort)
인덱스를 설정하여 현재 위치의 값을 아래쪽으로 순회하며 알맞은 곳에 넣어준다.
이미 정렬이 되어있다면 O(n)의 시간 복잡도를 가지게 된다. 정렬이 되어있는 경우라면 한 번 순회하며 체크만 하기 때문이며, 시간 복잡도는 O(n^2)이다
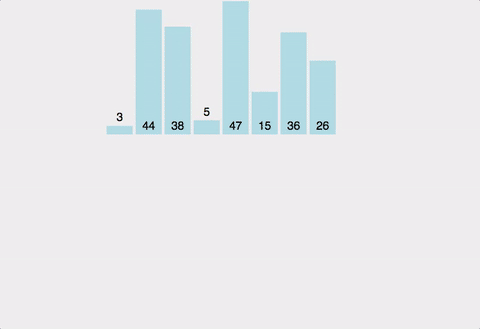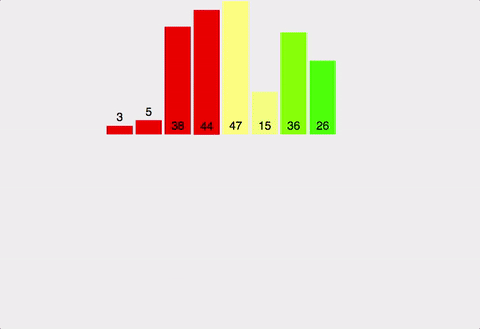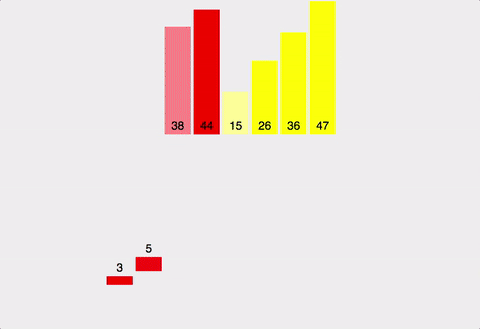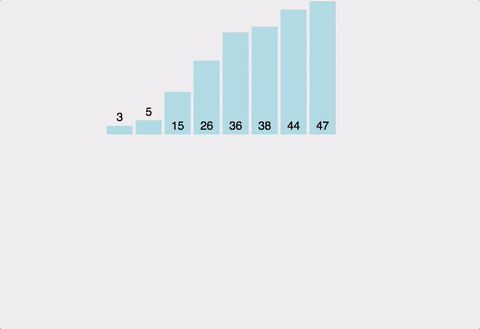
def insertionSort(alist): for index in range(1,len(alist)): currentvalue = alist[index] position = index while position>0 and alist[position-1]>currentvalue: alist[position]=alist[position-1] position = position-1 alist[position]=currentvalue return alist
​
4. 병합 정렬(Merge sort)
정렬한 리스트를 반으로 쪼개며 좌우 리스트를 분할해 정렬 후 병합한다. 가장 많이 쓰이는 정렬 중 하나, 시간 복잡도는 최소 O(nlogn)을 보장하게 된다.
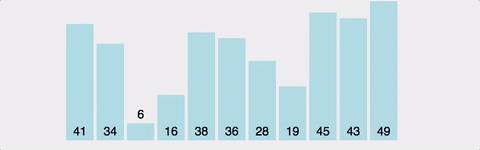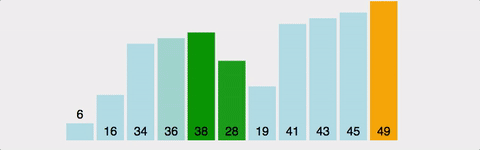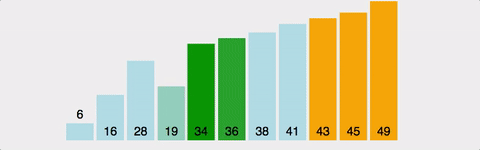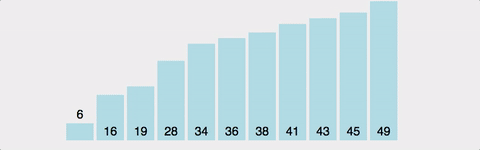
def mergeSort(alist): if len(alist) <= 1: return alist mid = len(alist) // 2 leftlist = alist[:mid] rightlist = alist[mid:] L = mergeSort(leftlist) R = mergeSort(rightlist) i = j = 0 result = [] while i < len(L) and j < len(R): if L[i] < R[j]: result.append(L[i]) i+=1 else: result.append(R[j]) j+=1 result += L[i:] result += R[j:] return result
​
5. 힙 정렬
힙이라는 자료구조를 통해 내림차순으로 숫자를 넣은 후, 역순으로 꺼내어 정렬한다.
​
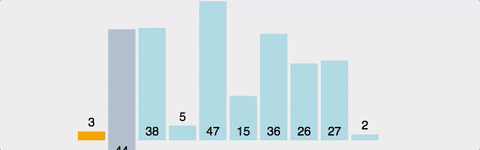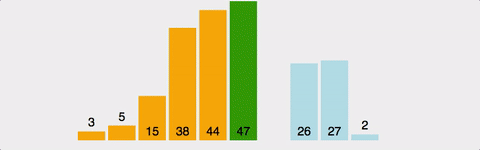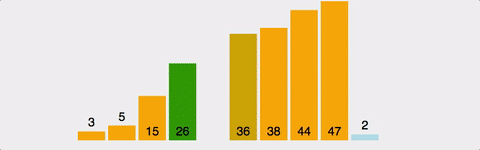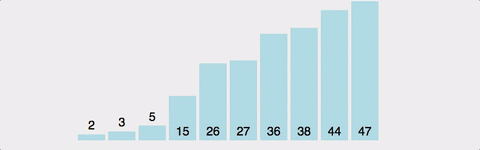
6. 퀵 정렬(Quick sort)
pivot 기준으로 좌측과 우측으로 작은 값과 큰 값을 재배치하고 분할하여 정렬한다. 최악의 경우에는 O(n^2)의 비교를 수행하지만 일반적으로 O(nlogn)의 시간 복잡도를 가진다.
def partition(alist, start, end): pivot = alist[start] left = start+1 right = end done = False while not done: while left <= right and alist[left] <= pivot: left += 1 while alist[right] >= pivot and right >= left: right -= 1 if right < left: done = True else: tmp = alist[left] alist[left] = alist[right] alist[right] = tmp tmp = alist[start] alist[start] = alist[right] alist[right] = tmp return right def quickSort(alist, start, end): if start < end: pivot = partition(alist, start, end) quickSort(alist, start, pivot-1) quickSort(alist, pivot+1, end) return alist
​
​
​
*도움이 되는 사이트 및 출처
​

[Algorithm] 알고리즘 공부 시작 방법 및 순서
About Posts Study Note Tags [Algorithm] 알고리즘 공부 시작 방법 및 순서 by Yena Choi Study Note 개발 관련 공부한 내용을 정리한 포스트입니다. 오류 지적이나 제안 환영합니다. I wrote this post to summary what I studied on development. Please feel free to correct my error. 2018-11-14 in Studynote 초보자 입장에서 알고리즘 공부를 시작하고 싶어서 뭐부터 해야 좋을지 조사하다가, 자료가 좀 ...
blog.yena.io
​
​
​
​
​
여러분의 댓글과 관심은 직장 노예의 엔도르핀이 됩니다 :)
​
​
​
​
​
​
​
​
​
​
Instagram @ turtle__ju
Facebook @ https://www.facebook.com/100005591914690
라벨:

댓글

댓글 쓰기

가장 많이 본 글